Douglas' lemma

In operator theory, an area of mathematics, Douglas' lemma relates factorization, range inclusion, and majorization of Hilbert space operators. It is generally attributed to Ronald G. Douglas, although Douglas acknowledges that aspects of the result may already have been known. The statement of the result is as follows:

Theorem: If A and B are bounded operators on a Hilbert space H, the following are equivalent:

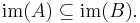
$\text{im}(A)\subseteq\text{im}(B).\,$
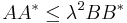$AA^*\leq\lambda^2 BB^*$ for some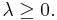 $\lambda\geq 0.\,$
There exists a bounded operator C on H such that A = BC.

Moreover, if these equivalent conditions hold, then there is a unique operator C such that

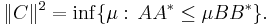
$\Vert C \Vert^2=\inf\{\mu�:\,AA^*\leq\mu BB^*\}.$
ker(A) = ker(C)
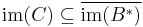
$\text{im}(C)\subseteq\overline{\text{im}(B^*)}$

References

Douglas, R.G.: "On Majorization, Factorization, and Range Inclusion of Operators on Hilbert Space". Proceedings of the American Mathematical Society 17, 413–415 (1966)

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Douglas' lemma

See also

References